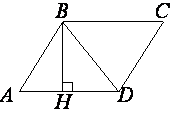Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=6 и HD=75. Диагональ параллелограмма BD равна 85. Найдите площадь параллелограмма.
Площадь
параллелограмма равна произведению высоты на сторону параллелограмма. Sпараллелограмма=BH*AD
Найдем высоту. По
теореме Пифагора запишем:
BD2=HD2+BH2
852=752+BH2
7225=5625+BH2
BH2=1600
BH=40
Sпараллелограмма=BH*AD=BH*(AH+HD)=40*(6+75)=40*81=3240
Ответ: Sпараллелограмма=3240
Поделитесь решением
Присоединяйтесь к нам...
В трапеции ABCD AB=CD, ∠BDA=54° и ∠BDC=33°. Найдите угол ABD. Ответ дайте в градусах.
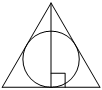Радиус окружности, вписанной в равносторонний треугольник, равен 12. Найдите высоту этого треугольника.
В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 30°. Найдите величину угла OAB.
В треугольнике со сторонами 2 и 4 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 2. Чему равна высота, проведённая ко второй стороне?
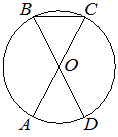В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 50°. Найдите угол ACB. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: