
 В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 75°. Найдите величину угла ODC.
В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 75°. Найдите величину угла ODC.
Рассмотрим треугольник АОВ. Этот треугольник
равнобедренный, т.к. ОА и ОВ - радиусы, поэтому они равны.
По
свойству равнобедренного треугольника /OAB=/OBA.
Рассмотрим треугольники АОВ и COD. /DOC=/AOB, т.к. они
вертикальные. СО=DO=OB=OA, т.к. это радиусы окружности.
Следовательно, треугольники АОВ и COD равны (по
первому признаку). Поэтому /OBA=/OAB=/ODC=/OCD=75°
Ответ: /ODC=75°.
Поделитесь решением
Присоединяйтесь к нам...
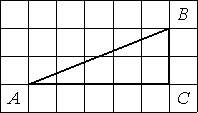 Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
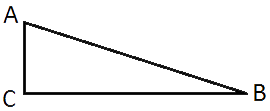 Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 40 и 85.
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 40 и 85.
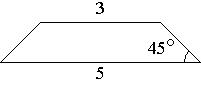 В равнобедренной трапеции основания равны 3 и 5, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
В равнобедренной трапеции основания равны 3 и 5, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
 В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен
45°. Найдите площадь трапеции.
В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен
45°. Найдите площадь трапеции.
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Комментарии:
(2016-04-18 13:33:01) Администратор: User, эти углы принадлежат разным секущим, поэтому они не являются внутренними накрест лежащими. К тому же, что бы говорить о накрест лежащих углах, надо доказать, что CD и AB параллельны.
(2016-04-16 09:18:47) User: Это внутренние накрест лежащие углы. ABO = ODC.