
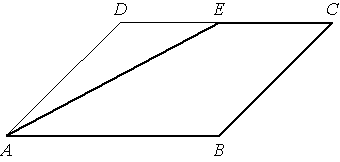
 Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB.
Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB.
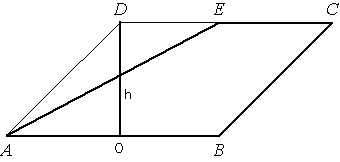 Проведем высоту
параллелограмма DO, как показано на рисунке. Площадь параллелограмма равна произведению стороны на высоту
параллелограмма.
Проведем высоту
параллелограмма DO, как показано на рисунке. Площадь параллелограмма равна произведению стороны на высоту
параллелограмма.Прислал пользователь Юлия
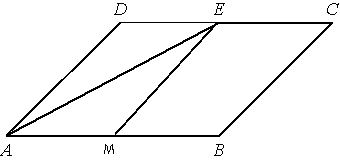 1) Отметим точку М на АB, так чтобы AM=MB
1) Отметим точку М на АB, так чтобы AM=MBПоделитесь решением
Присоединяйтесь к нам...
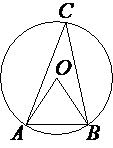 Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 27°.
Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 27°.
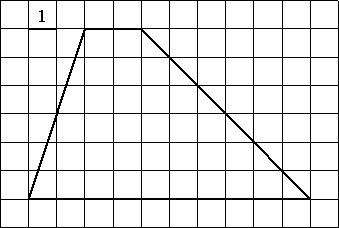 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
 В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=48 и CH=2. Найдите cosB.
В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=48 и CH=2. Найдите cosB.
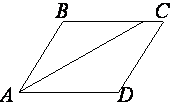 Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 14°. Ответ дайте в градусах.
Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 14°. Ответ дайте в градусах.
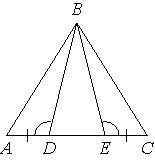 На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
Комментарии: