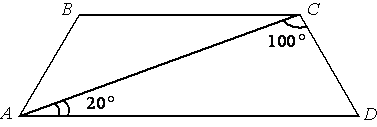
Найдите угол АВС равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.
AD||BC (по
определению трапеции). Тогда AC является секущей для этих параллельных отрезков.
/BCA=/CAD, т.к. они
внутренние накрест-лежащие.
Тогда /BCD=20°+100°=120°.
По
свойству
равнобедренной трапеции /ABC=/BCD=120°.
Ответ: /ABC=120°.
Поделитесь решением
Присоединяйтесь к нам...
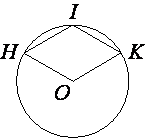Точка O – центр окружности, на которой лежат точки H, I и K таким образом, что OHIK – ромб. Найдите угол OKI. Ответ дайте в градусах.
Длина хорды окружности равна 60, а расстояние от центра окружности до этой хорды равно 40. Найдите диаметр окружности.
Найдите площадь параллелограмма, изображённого на рисунке.
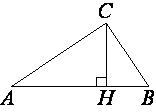В прямоугольном треугольнике ABC катет AC=35, а высота CH, опущенная на гипотенузу, равна 14√
Найдите площадь квадрата, если его диагональ равна 1.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: