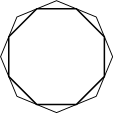
Дан правильный восьмиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный восьмиугольник.
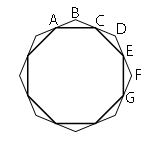Так как углы меньшего многоугольника располагаются на середине сторон, а сторон восемь, значит и углов будет восемь. Т.е. меньший многоугольник является восьмиугольником. Теперь докажем, что он правильный.
Рассмотрим треугольники ABC, CDE и EFG. AB=BC=CD=DE=EF=FG (по
определению правильного многоугольника).
/ABC=/CDE=/EFG (по
определению правильного многоугольника).
Следовательно, рассматриваемые треугольники равны (по
первому признаку равенства треугольников).
Это означает, что AC=CE=EG=GA.
Из равенства этих треугольников также следует, что все их острые углы тоже равны (/BAC=/BCA=/DCE=...и т.д.). Следовательно, /ACE=/CEG=...и так далее
В итоге, по
определению правильного многоугольника получается, меньший восьмиугольник - правильный.
Поделитесь решением
Присоединяйтесь к нам...
Основания трапеции относятся как 2:3. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. В каком отношении эта прямая делит площадь трапеции?
Какие из данных утверждений верны? Запишите их номера.
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) Если в ромбе один из углов равен
90°, то такой ромб — квадрат.
В окружности с центром в точке О проведены диаметры AD и BC, угол
ABO равен 30°. Найдите величину угла ODC.
Найдите площадь треугольника, изображённого на рисунке.
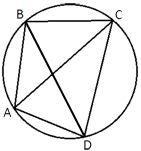Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: