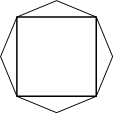
Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат.
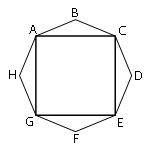Рассмотрим треугольники ABC, CDE, EFG и GHA. AB=BC=CD=DE=EF=FG=GH=HA (по
определению правильного многоугольника).
/ABC=/CDE=/EFG=/GHA (по
определению правильного многоугольника).
Следовательно, рассматриваемые треугольники равны (по
первому признаку равенства треугольников).
Это означает, что AC=CE=EG=GA.
Из равенства этих треугольников также следует, что все их острые углы тоже равны (/BAC=/BCA=/DCE=...и т.д.). Следовательно, /ACE=/CEG=/EGA=/GAC.
В итоге, по
определению правильного многоугольника получается, что ACEG - правильный многоугольник. А т.к. этот многоугольник имеет 4 угла, то это
квадрат.
Поделитесь решением
Присоединяйтесь к нам...
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=27, CM=9. Найдите AO.
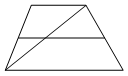Основания трапеции равны 8 и 18. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
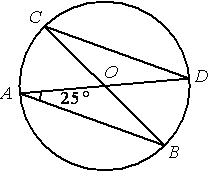В окружности с центром в точке О проведены диаметры AD и BC, угол OAB равен 25°. Найдите величину угла OCD.
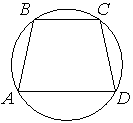Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 32°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Найдите площадь параллелограмма, изображённого на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: