
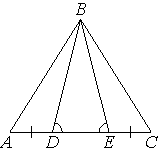
 На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АEB и BDC тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АEB и BDC тоже равны. Докажите, что треугольник АВС — равнобедренный.
1) По условию задачи /BED=/EDB, следовательно треугольник BDE - равнобедренный (по
свойству). По
определению равнобедренного треугольника BE=BD.
Смежные углы для углов /BED и /EDB тоже равны, /BDA=/BEC.
2) Рассмотрим треугольники ABD и CBE.
AD=EC (по условию),
BE=BD (согласно п.1),
/BDA=/BEC (из п.1),
следовательно эти треугольники равны (по
первому признаку равенства треугольников), а это значит, что BA=BC. Следовательно треугольник ABC - равнобедренный (по
определению).
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC угол C равен 90°, sinA=4/5, AC=9. Найдите AB.
В треугольнике ABC угол C равен 90°, sinA=4/5, AC=9. Найдите AB.
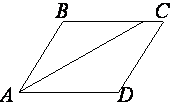 Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 14°. Ответ дайте в градусах.
Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 14°. Ответ дайте в градусах.
 Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 9 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
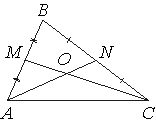 Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=18, CM=21. Найдите OM.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=18, CM=21. Найдите OM.
Комментарии: