В треугольнике ABC угол C прямой, BC=6, cosB=0,3. Найдите AB.
По
определению косинуса cosB=BC/AB => AB=BC/cosB=6/0,3=20.
Ответ: AB=20.
Поделитесь решением
Присоединяйтесь к нам...
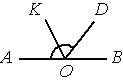Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=64°. Ответ дайте в градусах.
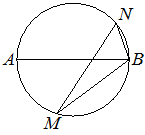На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=69°. Найдите угол NMB. Ответ дайте в градусах.
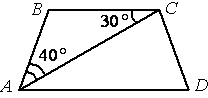Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
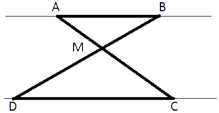Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=16, DC=24, AC=25.
Укажите номера верных утверждений.
1) Центр описанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Квадрат является прямоугольником.
3) Сумма углов любого треугольника равна
180°.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: