
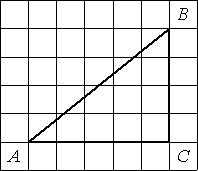
 Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
По
определению тангенса: tgA=BC/AC=4/5=0,8.
Ответ: tgB=0,8.
Поделитесь решением
Присоединяйтесь к нам...
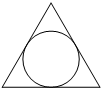 Радиус окружности, вписанной в равносторонний треугольник, равен 2√
Радиус окружности, вписанной в равносторонний треугольник, равен 2√
 Площадь прямоугольного треугольника равна 50√
Площадь прямоугольного треугольника равна 50√
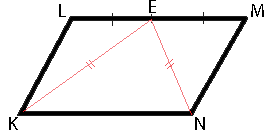 В параллелограмме KLMN точка E — середина стороны LM. Известно, что EK=EN. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме KLMN точка E — середина стороны LM. Известно, что EK=EN. Докажите, что данный параллелограмм — прямоугольник.
Укажите номера верных утверждений.
1) Если один из углов треугольника прямой, то треугольник прямоугольный.
2) Диагонали квадрата точкой пересечения делятся пополам.
3) Точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к этому отрезку.
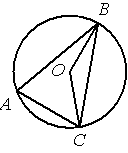 Точка О – центр окружности, /BAC=70° (см. рисунок). Найдите величину угла BOC (в градусах).
Точка О – центр окружности, /BAC=70° (см. рисунок). Найдите величину угла BOC (в градусах).
Комментарии: