
Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является его медианой.
Рассмотрим каждое утверждение:
1) "Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны". Это утверждение верно по
первому признаку подобия.
2) "Вертикальные углы равны", это утверждение верно, по
свойству углов.
3) "Любая биссектриса равнобедренного треугольника является его медианой", это утверждение неверно, т.к., по
свойству равнобедренного треугольника, только
биссектриса, проведенная к основанию, совпадает с
медианой и высотой.
Поделитесь решением
Присоединяйтесь к нам...
 В окружности с центром в точке O проведены диаметры
AD и BC, угол OAB равен 70°. Найдите величину угла OCD.
В окружности с центром в точке O проведены диаметры
AD и BC, угол OAB равен 70°. Найдите величину угла OCD.
 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
 В равнобедренную трапецию, периметр которой равен 200, а площадь равна 2000, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
В равнобедренную трапецию, периметр которой равен 200, а площадь равна 2000, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
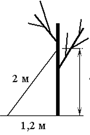 Лестницу длиной 2 м прислонили к дереву.
На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на
1,2 м?
Лестницу длиной 2 м прислонили к дереву.
На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на
1,2 м?
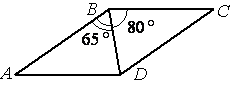 Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 80°. Найдите меньший угол параллелограмма.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 80°. Найдите меньший угол параллелограмма.
Комментарии:
(2017-01-26 23:57:40) Администратор: Анастасия, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2017-01-25 18:27:37) Анастасия: Какие из следующих утверждений верны? 1.Расстояние от точки, лежащей на окружности, до центра окружности равно радиусу. 2.Площади трапеции равна произведению основания трапеции на высоты. 3.Треугольника со сторонами 1,2,4 не существуют.