Укажите номера верных утверждений.
1) Любой квадрат является ромбом.
2) Против равных сторон треугольника лежат равные углы.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
Рассмотрим каждое утверждение:
1) "Любой квадрат является ромбом", это утверждение верно, т.к.
квадрат удовлетворяет определению
ромба.
2) "Против равных сторон треугольника лежат равные углы", это утверждение верно (по свойству
равнобедренного и
равностороннего треугольников).
3) "Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности", это утверждение верно. Эта система (точка и окружность) имеет
ось симметрии - прямая проведенная через данную точку и центр окружности. Соответственно, если можно провести одну
касательную, то можно провести и вторую, симметричную первой.
Ответ: 1), 2) и 3)
Поделитесь решением
Присоединяйтесь к нам...
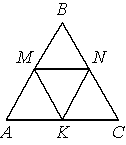В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.
В треугольнике ABC угол C равен 90°, sinB=4/9, AB=18. Найдите AC.
Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 1,8 м, высота большой опоры 2,8 м. Найдите высоту средней опоры.
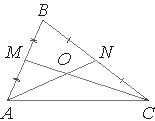Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=12, CM=18. Найдите AO.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=26.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: