
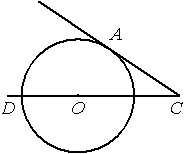
 Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
130°.
Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
130°.
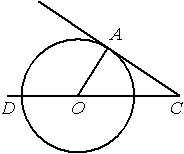 Проведем отрезок ОА.
Проведем отрезок ОА.
/DOA -
центральный угол для данной окружности. Он опирается на дугу AD, равную 130°. Следовательно, /DOA тоже равен 130°.
/AOC -
смежный углу DOA, поэтому /AOC=180°- /DOA=180°-130°=50°.
Треугольник ACO -
прямоугольный, т.к. радиус всегда перпендикулярен
касательной (по
свойству касательной). Т.е. /ОАС=90°. Применяя
теорему о сумме углов треугольника, можем записать:
180°=/AСO+/CAO+/AOC.
/AСO=180°-/CAO-/AOC=180°-90°-50°=40°.
Ответ: /ACO=40°.
Поделитесь решением
Присоединяйтесь к нам...
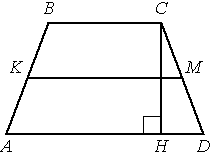 В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 4.
В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 4.
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=36, MN=27. Площадь треугольника ABC равна 96. Найдите площадь треугольника MBN.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=36, MN=27. Площадь треугольника ABC равна 96. Найдите площадь треугольника MBN.
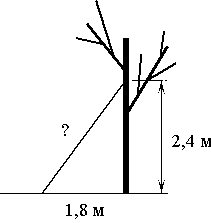 Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 2,4 м над землёй, а нижний отстоит от ствола дерева на 1,8 м?
Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 2,4 м над землёй, а нижний отстоит от ствола дерева на 1,8 м?
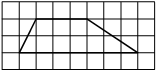 На клетчатой бумаге с размером клетки 1x1 изображена трапеция. Найдите её площадь.
На клетчатой бумаге с размером клетки 1x1 изображена трапеция. Найдите её площадь.
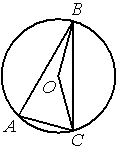 Точка О — центр окружности, ∠BOC=160°. Найдите величину угла BAC (в градусах).
Точка О — центр окружности, ∠BOC=160°. Найдите величину угла BAC (в градусах).
Комментарии: