Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=36, MN=27. Площадь треугольника ABC равна 96. Найдите площадь треугольника MBN.
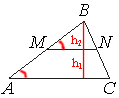Рассмотрим треугольники ABC и MBN.
∠ABC - общий.
∠BAC=∠BMN
Следовательно, по первому признаку подобия, эти треугольники подобны.
Площади треугольника ABC:
SABC=(1/2)AC*h1
96=(1/2)*36*h1
h1=96*2/36=96/18=32/6
Из подобия треугольников получаем пропорцию:
AC/MN=h1/h2
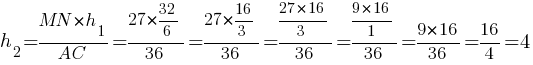
Тогда площадь треугольника MBN:
SMBN=(1/2)MN*h2
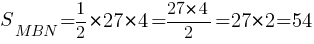
Ответ: 54
Поделитесь решением
Присоединяйтесь к нам...
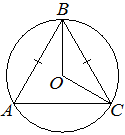Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=57°. Найдите величину угла BOC. Ответ дайте в градусах.
К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=40, AO=85.
Радиус окружности, описанной около квадрата, равен 38√2. Найдите радиус окружности, вписанной в этот квадрат.
Две трубы, диаметры которых равны 7 см и 24 см, требуется заменить одной, площадь поперечного сечения которой равна сумме площадей поперечных сечений двух данных. Каким должен быть диаметр новой трубы? Ответ дайте в сантиметрах.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 1. Найдите площадь трапеции.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: