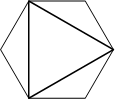
Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
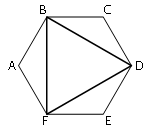Рассмотрим треугольники FAB, BCD и DEF.
Т.к. шестиугольник
правильный, то FA=AB=BC=CD=DE=EF и углы /FAB=/BCD=/DEF. Значит рассматриваемые треугольники равны (по
первому признаку равенства). Следовательно, FB=BD=DF. Т.е. треугольник BDF -
равносторонний.
Поделитесь решением
Присоединяйтесь к нам...
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника BKP к площади треугольника AMK.
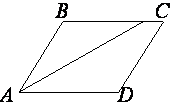Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 1°. Ответ дайте в градусах.
Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является его медианой.
Сторона ромба равна 36, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Радиус окружности, описанной около квадрата, равен 16√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: