
Укажите номера верных утверждений.
1) Центр описанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Квадрат является прямоугольником.
3) Сумма углов любого треугольника равна
180°.
Рассмотрим каждое утверждение:
1) "Центр описанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника".
Высота, проведенная к основанию является и
медианой, и биссектрисой (по
свойству равнобедренного треугольника), т.е. является
серединным перпендикуляром. А центром описанной окружности является точка пересечения
серединных перпендикуляров (
теорема об описанной окружности). Следовательно, это утверждение верно.
2) "Квадрат является прямоугольником", это утверждение верно (по
определению).
3) "Сумма углов любого треугольника равна 180°", это утверждение верно (по
теореме).
Поделитесь решением
Присоединяйтесь к нам...
 Радиус окружности с центром в точке O равен 85, длина хорды AB равна 80. Найдите расстояние от хорды AB до параллельной ей касательной k.
Радиус окружности с центром в точке O равен 85, длина хорды AB равна 80. Найдите расстояние от хорды AB до параллельной ей касательной k.
 В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 17:15, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=16.
В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 17:15, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=16.
 Боковые стороны AB и CD трапеции ABCD равны соответственно 20 и 25, а основание BC равно 5. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Боковые стороны AB и CD трапеции ABCD равны соответственно 20 и 25, а основание BC равно 5. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
 На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.
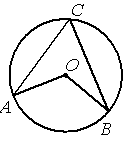 Точка О – центр окружности, /ACB=65° (см. рисунок). Найдите величину угла AOB (в градусах).
Точка О – центр окружности, /ACB=65° (см. рисунок). Найдите величину угла AOB (в градусах).
Комментарии: