
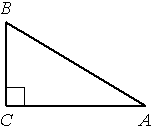
 В треугольнике ABC угол C прямой, BC=9, sinA=0,3. Найдите AB.
В треугольнике ABC угол C прямой, BC=9, sinA=0,3. Найдите AB.
По
определению синуса sinA=BC/AB => AB=BC/sinA=9/0,3=30.
Ответ: AB=30.
Поделитесь решением
Присоединяйтесь к нам...
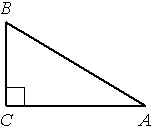 В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB.
В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB.
 Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 9 и 11 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=√
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 9 и 11 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=√
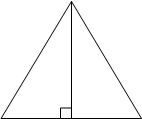 Высота равностороннего треугольника равна
15√
Высота равностороннего треугольника равна
15√
 На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 4 м?
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 4 м?
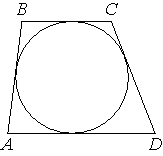 Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=13, CD=22. Найдите AD.
Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=13, CD=22. Найдите AD.
Комментарии: