
 Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 9 и 11 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=√
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 9 и 11 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=√
Вариант №1 (прислал Всеволод).
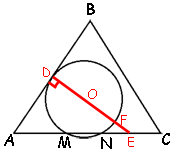 Проведем отрезок от точки касания стороны AB и окружности через центр окружности к стороне AC. Обозначим точки как показано на рисунке.
Проведем отрезок от точки касания стороны AB и окружности через центр окружности к стороне AC. Обозначим точки как показано на рисунке.
AD2=AM*AN (по
теореме о касательно и секущей для точки А).
AD2=9*11=99
AD=√
Рассмотрим треугольник ADE.
Данный треугольник
прямоугольный (по
свойству касательной).
cos∠BAC=AD/AE (по
определению).
AE=AD/cos∠BAC=3√
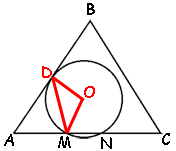 Дополнительно обозначим ключевые точки и проведем отрезки, как показано на рисунке.
Дополнительно обозначим ключевые точки и проведем отрезки, как показано на рисунке.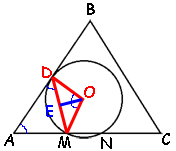 По
четвертому свойству углов, связанных с окружностью ∠ADM равен половине градусной меры дуги DM.
По
четвертому свойству углов, связанных с окружностью ∠ADM равен половине градусной меры дуги DM.Поделитесь решением
Присоединяйтесь к нам...
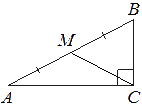 В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=20, BC=10. Найдите CM.
В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=20, BC=10. Найдите CM.
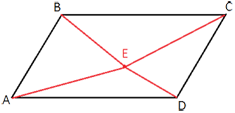 Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
 Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 44°, 71° и 65°.
Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 44°, 71° и 65°.
 Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
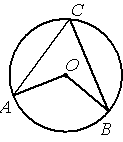 Точка О – центр окружности, /AOB=128° (см. рисунок). Найдите величину угла ACB (в градусах).
Точка О – центр окружности, /AOB=128° (см. рисунок). Найдите величину угла ACB (в градусах).
Комментарии:
(2017-05-03 21:11:28) Администратор: Василина, cos∠DOE=cos∠BAC, так как ∠DOE=∠BAC. В решении это показано.
(2017-05-02 22:31:56) Администратор: Анатолий, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправте заявку на добавление задачи, и мы ее обязательно добавим.
(2017-05-01 12:54:15) анатолий: в основании пирамиды лежит квадрат.одна из боковых граней перпендикулярна ее основанию а две соседние с ней грани образуют с основанием двугранные углы по 30.найти площадь поверхности пирамиды если ее высота равна h
(2017-04-18 14:36:53) Генрих: Пару дней назад все выслал)
(2017-04-13 12:28:20) Генрих: Все красиво перепишу и постараюсь сегодня выслать)
(2017-04-03 12:06:06) Администратор: Генрих, здравствуйте! Присылайте на admin@otvet-gotov.ru, будем очень благодарны!
(2017-04-03 12:04:55) Администратор: Генрих, здравствуйте! Присылайте на admin@otvet-gotov.ru, будем очень благодарны!
(2017-04-03 03:39:16) Генрих: Здравствуйте, хотел бы поделиться другим решением, куда его можно прислать, мне кажется, оно более универсально.
(2016-02-09 00:51:04) Администратор: Ксения, да, Вы правы, я подумаю, над этим вопросом...Спасибо за информацию.
(2016-02-09 00:41:58) Ксения: опечатка в моем комментарии: косинус=(корень из 15, деленный на 4(!)
(2016-02-09 00:37:24) Ксения: Решала аналогичную задачу с другими цифрами (расстояния 12 и 45 соответственно, косинус=(корень из 15, деленный на 2) первым способом. Получилось, что АЕ=24, что противоречит условию, т.к. АЕ должно быть больше, чем 45... Получается, что решение подходит не для всех задач..
(2015-05-26 17:22:14) Денис: моя задача на пробном ОГЭ (ГИА) в этом году.. аж до сих пор её помню)
(2015-05-05 09:53:28) Администратор: Галина, Вы меня запутали ))) Все нормально в этом варианте. Посмотрите свой же комментарий "АЕ=18, при этом по условию AM=9, AN=11, т.е. AN=20", у Вас AN то равняется 11, то 20...По условию AN=11, значит AE больше, чем AN...
(2015-05-05 09:49:56) Администратор: Галина, да, интересное замечание, я как-то даже не обратил внимания...Спасибо, я подумаю над этим вопросом...
(2015-05-05 09:11:30) Галина: Для варианта №1 АЕ=18, при этом по условию AM=9, AN=11, т.е. AN=20. Т.е. вторая часть решения EN*EM=EF*DE теряет смысл.