Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника AKM к площади четырёхугольника KPCM.
BM -
медиана треугольника АВС,
следовательно, она делит этот треугольник на два равных по площади треугольника (
свойство медианы).
SABM=SCMB=SABC/2
Рассмотрим треугольник ABM.
SABK+SAKM=SABM=SABC/2
AP -
биссектриса, по
теореме о биссектрисе можно записать AM/AB=KM/BK.
По условию задачи AC втрое больше AB, следовательно, AM в 1,5 раза больше АВ (т.к. является половиной АС)
KM/BK=1,5. Т.к. площадь треугольника вычисляется по формуле S=1/2*h*a, где а-основание и h-высота,
то можем записать:
SAKM=1/2*h*KM=1/2*h*(1,5*BK),
SAKM=1/2*h*(3/2*BK)=3/2*(1/2*h*BK)=3/2*SABK (т.к. высота h для этих треугольников общая)
SABK=2/3*SAKM
SABK+SAKM=SABM=SABC/2
2/3*SAKM+SAKM=SABC/2
5/3*SAKM=SABC/2
SAKM=0,3*SABC
По тому же
свойству биссектрисы для треугольника ABC получаем, что AC/AB=CP/PB
AC/AB=3 (по условию задачи), следовательно, CP=3*PB
SAPC=1/2*h*PC=1/2*h*(3*PB)=3*(1/2*h*PB)=3*SABP,
SABP+SAPC=SABC
SABP+3*SABP=SABC
SABP=SABC/4
SKPCM=SABC-SABP-SAKM=SABC-SABC/4-0,3*SABC=0,45*SABC
Отношение SAKM к SKPCM равно 0,3*SABC/0,45*SABC=2/3
Ответ: Отношение SAKM к SKPCM равно 2/3.
Поделитесь решением
Присоединяйтесь к нам...
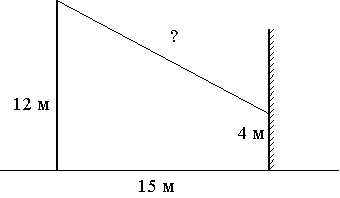От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода. Ответ дайте в метрах.
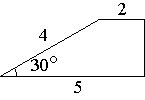Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен
30°. Найдите площадь трапеции, если её основания равны 2 и 5.
Какие из данных утверждений верны? Запишите их номера.
1) Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны.
2) В любой четырёхугольник можно вписать окружность.
3) Центром описанной окружности треугольника является точка пересечения серединных перпендикуляров к его сторонам.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен
60°, а радиус окружности равен 6.
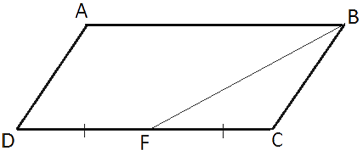Сторона CD параллелограмма ABCD вдвое больше стороны BC. Точка F — середина стороны CD. Докажите, что BF — биссектриса угла ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: