
 В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
По
теореме о сумме углов треугольника: 180°=/A+/B+/C, отсюда /B=180°-/A-/C=180°-20°-60°=100°.
/ABD=/B/2=50° (т.к. BD -
биссектриса).
Рассмотрим треугольник BHC, по
теореме о сумме углов треугольника получаем 180°=60°+90°+/CBH => /CBH=30°.
Тогда искомый угол /DBH=/B-/ABD-/CBH=100°-50°-30°=20°.
Ответ: /DBH=20°
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC известно, что AB=BC, ∠ABC=102°. Найдите угол BCA. Ответ дайте в градусах.
В треугольнике ABC известно, что AB=BC, ∠ABC=102°. Найдите угол BCA. Ответ дайте в градусах.
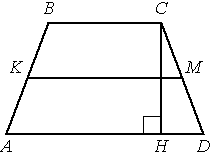 В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 4.
В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 4.
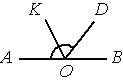 Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=64°. Ответ дайте в градусах.
Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=64°. Ответ дайте в градусах.
 Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 7:6, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 48.
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 7:6, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 48.
 На стороне AB треугольника ABC взята такая точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=40, BC=45 и CD=24.
На стороне AB треугольника ABC взята такая точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=40, BC=45 и CD=24.
Комментарии:
(2016-03-13 23:54:51) Администратор: Спасибо за найденную опечатку, исправлено.
(2016-03-12 14:31:32) : Исправьте, пожалуйста, в ответе угол СВН на DBH.