Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны.
2) В любой четырёхугольник можно вписать окружность.
3) Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника.
Рассмотрим каждое утверждение.
1) "Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны", это утверждение верно по
свойствам углов.
2)"В любой четырёхугольник можно вписать окружность", это утверждение неверно, т.к. должны выполниться
определенные условия.
3) "Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника", это утверждение верно, по
теореме об описанной окружности.
Поделитесь решением
Присоединяйтесь к нам...
Сторона квадрата равна 3√2. Найдите диагональ этого квадрата.
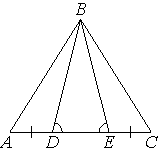На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АEB и BDC тоже равны. Докажите, что треугольник АВС — равнобедренный.
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=79°. Найдите величину угла BOC. Ответ дайте в градусах.
Какие из данных утверждений верны? Запишите их номера.
1) На плоскости существует единственная точка, равноудалённая от концов отрезка.
2) В любой треугольник можно вписать окружность.
3) Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.
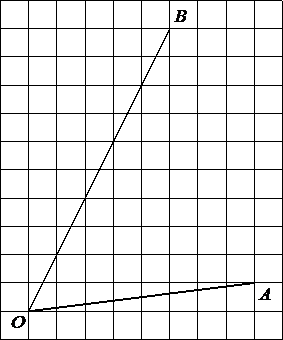Найдите тангенс угла
AOB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: