
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны.
2) В любой треугольник можно вписать окружность.
3) Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.
Рассмотрим каждое утверждение.
1) "Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны", это утверждение верно по
свойствам углов.
2) "В любой треугольник можно вписать окружность", это утверждение верно по свойству вписанной окружности.
3) "Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом". По
свойству параллелограмма, противоположные стороны попарно равны. А раз смежные стороны равны, то и противоположные им стороны так же равны. Таким образом получается, что все четыре стороны такого параллелограмма равны. А это и есть
определение ромба.
Поделитесь решением
Присоединяйтесь к нам...
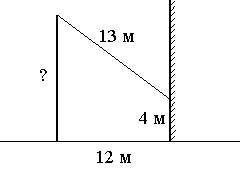 От столба к дому натянут провод длиной 13 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
От столба к дому натянут провод длиной 13 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
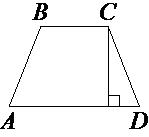 Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 1 и 5. Найдите длину основания BC.
Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 1 и 5. Найдите длину основания BC.
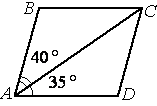 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 40° и 35°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 40° и 35°. Найдите больший угол параллелограмма.
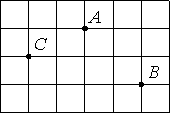 На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
 Радиус окружности, описанной около квадрата, равен 16√
Радиус окружности, описанной около квадрата, равен 16√
Комментарии: