Какие из данных утверждений верны? Запишите их номера.
1) Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны.
2) В любой четырёхугольник можно вписать окружность.
3) Центром описанной окружности треугольника является точка пересечения серединных перпендикуляров к его сторонам.
Рассмотрим каждое утверждение.
1) "Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны"? это утверждение верно по
первому признаку подобия.
2)"В любой четырёхугольник можно вписать окружность", это утверждение неверно, т.к. есть
определенные условия, при которых можно окружность вписать в четырехугольник.
3) "Центром описанной окружности треугольника является точка пересечения серединных перпендикуляров к его сторонам", это утверждение верно по свойствам описанной окружности.
Поделитесь решением
Присоединяйтесь к нам...
Точка О – центр окружности, /BOC=110° (см. рисунок). Найдите величину угла BAC (в градусах).
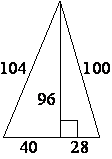Найдите площадь треугольника, изображённого на рисунке.
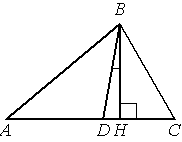В треугольнике АВС углы А и С равны 40° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
Какие из данных утверждений верны? Запишите их номера.
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) Если в ромбе один из углов равен
90°, то такой ромб — квадрат.
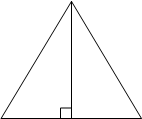Высота равностороннего треугольника равна 96√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: