Какие из данных утверждений верны? Запишите их номера.
1) Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны.
2) В любой четырёхугольник можно вписать окружность.
3) Центром описанной окружности треугольника является точка пересечения серединных перпендикуляров к его сторонам.
Рассмотрим каждое утверждение.
1) "Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны"? это утверждение верно по
первому признаку подобия.
2)"В любой четырёхугольник можно вписать окружность", это утверждение неверно, т.к. есть
определенные условия, при которых можно окружность вписать в четырехугольник.
3) "Центром описанной окружности треугольника является точка пересечения серединных перпендикуляров к его сторонам", это утверждение верно по свойствам описанной окружности.
Поделитесь решением
Присоединяйтесь к нам...
Сторона равностороннего треугольника равна 10√
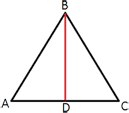
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=44, MN=24. Площадь треугольника ABC равна 121. Найдите площадь треугольника MBN.
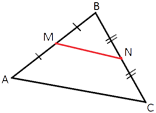Точки M и N являются серединами сторон AB и BC треугольника ABC, AC=42. Найдите MN.
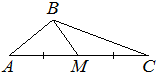В треугольнике ABC известно, что AC=38, BM — медиана, BM=17. Найдите AM.
Какое из следующих утверждений верно?
1) Площадь квадрата равна произведению двух его смежных сторон.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: