Точка О – центр окружности, /BOC=110° (см. рисунок). Найдите величину угла BAC (в градусах).
По условию /BOC=110°, этот угол является
центральным, соответственно дуга ВC тоже равна 110°. /BAC - является
вписанным углом и равен половине дуги, на которую опирается (по теореме о вписанном угле). Соответственно, 110/2=55.
Ответ: /BAC=55°.
Поделитесь решением
Присоединяйтесь к нам...
Окружности радиусов 3 и 33 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
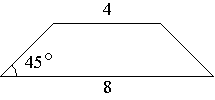В равнобедренной трапеции основания равны 4 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
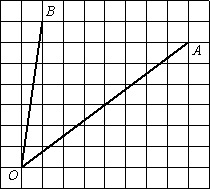Найдите тангенс угла AOB.
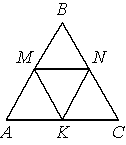В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.
В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=52 и CH=13. Найдите cosB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2021-09-28 11:08:19) Администратор: Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2021-04-29 07:48:56) : AB - диаметр окружности с центром в точке O. Если A (8, -3), B (-2, -5) найти координаты центра круга Напишите уравнение круга согласно пункту а).