Какие из данных утверждений верны? Запишите их номера.
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) Если в ромбе один из углов равен
90°, то такой ромб — квадрат.
Рассмотрим каждое утверждение.
1) "Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой", это утверждение верно по
свойству параллельных прямых.
2) "Треугольник со сторонами 1, 2, 4 существует", это утверждение неверно,т.к. длина одной из сторон не может быть больше суммы длин двух других сторон (а 4>1+2).
3) "Если в
ромбе один из углов равен
90°, то такой ромб — квадрат". Чтобы ромб был квадратом, необходимо, чтобы все 4 угла были равны 90°.
Т.к.
ромб - частный случай
параллелограмма, то к нему и применимы все
свойства параллелограмма, следовательно (по
свойству параллелограмма), противоположный прямому углу, угол тоже равен 90°.
Другие два угла по тому же свойству равны друг другу.
Сумма углов многоугольника вычисляется по формуле (n-2)*180°, где n - количество углов. В нашем случае, углов - 4. Тогда сумма углов равна (4-2)*180°=360°.
Тогда получается, что сумма двух неизвестных углов равна 360°-90°-90°=180°. А так как они равны друг другу, то каждый из них равен 180°/2=90°.
Т.е. мы узнали, что все четыре угла равны по 90°, следовательно это утверждение верно.
Поделитесь решением
Присоединяйтесь к нам...
В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 10, а меньшее основание BC равно 4.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 7.
Укажите номера верных утверждений.
1) В тупоугольном треугольнике все углы тупые.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
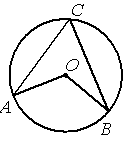Точка О – центр окружности, /BOC=60° (см. рисунок). Найдите величину угла BAC (в градусах).
Прямая касается окружности в точке K. Центр окружности – точка O. Хорда KM образует с касательной угол, равный 40°. Найдите величину угла KOM. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2014-11-04 14:54:06) Администратор: Галина, очень рад, что наш сайт Вам помог!
(2014-11-04 14:44:19) Галина: всё верно у меня стоит пять за все эти задания в том числе и это!