На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,6 м, если длина его тени равна 8 м, высота фонаря 5 м?
Перерисуем данный рисунок в виде треугольников и обозначим интересующие нас точки.
Рассмотрим треугольники ABC и DCE, эти треугольники
подобны, т.к. /C - общий, /B и /DEC - прямые, а углы A и EDC - равны, так как являются
соответственными.
Из подобия этих треугольников следует, что AB/DE=BC/EC,
AB/DE=(BE+EC)/EC, отсюда (AB*EC)/DE=BE+EC
BE=(AB*EC)/DE-EC
BE=(5*8)/1,6-8=17
Ответ: расстояние от фонаря до человека 17 м.
Поделитесь решением
Присоединяйтесь к нам...
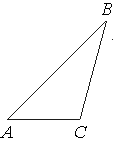В треугольнике ABC угол A равен 45°, угол B равен 30°, BC=6√
Центральный угол AOB равен
60°. Найдите длину хорды AB, на которую он опирается, если радиус окружности равен 7.
Найдите площадь параллелограмма, изображённого на рисунке.
Площадь равнобедренного треугольника равна 196√
Радиус окружности, описанной около равностороннего треугольника, равен 10. Найдите высоту этого треугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: