
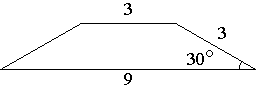
 Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
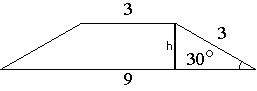 Площадь
трапеции равна произведению полусуммы оснований на высоту. Основания нам известны, найдем высоту трапеции.
Площадь
трапеции равна произведению полусуммы оснований на высоту. Основания нам известны, найдем высоту трапеции.
Проведем высоту как показано на рисунке. Получившийся треугольник является
прямоугольным. По
определению синуса можем записать: sin30°=h/3 => h=3*sin30°, sin30°=1/2 (
табличное значение).
h=3*1/2=1,5.
Sтрапеции=(3+9)/2*1,5=9
Ответ: площадь трапеции равна 9.
Поделитесь решением
Присоединяйтесь к нам...
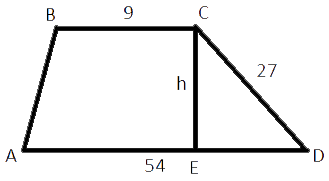 Основания трапеции равны 9 и 54, одна из боковых сторон равна 27, а косинус угла между ней и одним из оснований равен √
Основания трапеции равны 9 и 54, одна из боковых сторон равна 27, а косинус угла между ней и одним из оснований равен √
 Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 12 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 9 м. Найдите длину троса.
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 12 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 9 м. Найдите длину троса.
 Человек, рост которого равен 1,6 м, стоит на расстоянии 3 м от уличного фонаря. При этом длина тени человека равна 2 м. Определите высоту фонаря (в метрах).
Человек, рост которого равен 1,6 м, стоит на расстоянии 3 м от уличного фонаря. При этом длина тени человека равна 2 м. Определите высоту фонаря (в метрах).
 Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB=20, а расстояния от центра окружности до хорд AB и CD равны соответственно 24 и 10.
Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB=20, а расстояния от центра окружности до хорд AB и CD равны соответственно 24 и 10.
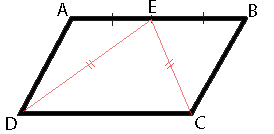 В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм - прямоугольник.
В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм - прямоугольник.
Комментарии: