
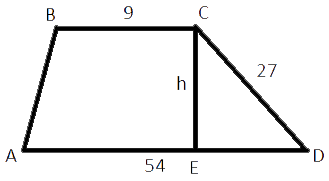
 Основания трапеции равны 9 и 54, одна из боковых сторон равна 27, а косинус угла между ней и одним из оснований равен √
Основания трапеции равны 9 и 54, одна из боковых сторон равна 27, а косинус угла между ней и одним из оснований равен √
Площадь
трапеции равна произведению полусуммы оснований на высоту. Основания нам известны, найдем высоту.
По
определению cos(/CDE)=ED/CD
√
ED=3*√
По
теореме Пифагора:
CD2=ED2+EC2
272=(3*√
729=9*65+EC2
EC2=144
EC=12 - это и есть высота
Sтрапеции=EC*(BC+AD)/2
Sтрапеции=12*(9+54)/2
Sтрапеции=6*63=378
Ответ: Sтрапеции=378
Поделитесь решением
Присоединяйтесь к нам...
 Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.
Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.
Стороны AC, AB, BC треугольника ABC равны 3√
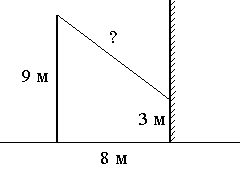 От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.
От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.
 В треугольнике ABC угол C равен 90°, sinA=0,75, AC=√
В треугольнике ABC угол C равен 90°, sinA=0,75, AC=√
 Радиус вписанной в квадрат окружности равен 7√
Радиус вписанной в квадрат окружности равен 7√
Комментарии: