
 Человек, рост которого равен 2 м, стоит на расстоянии 3,5 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).
Человек, рост которого равен 2 м, стоит на расстоянии 3,5 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).
 Перерисуем данный рисунок в виде треугольников и обозначим интересующие нас точки.
Перерисуем данный рисунок в виде треугольников и обозначим интересующие нас точки.
Рассмотрим треугольники ABC и DCE, эти треугольники
подобны, т.к. /C - общий, /B и /DEC - прямые, а углы A и EDC - равны, так как являются
соответственними.
Из подобия этих треугольников следует, что AB/DE=BC/EC, отсюда AB=(BC*DE)/EC=((3,5+1)*2)/1=9.
Ответ: высота фонаря равна 9 м.
Поделитесь решением
Присоединяйтесь к нам...
 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
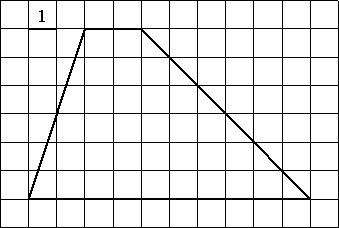 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
 В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=44, SQ=16.
В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=44, SQ=16.
 Радиус вписанной в квадрат окружности равен 14√
Радиус вписанной в квадрат окружности равен 14√
 Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 62°. Найдите величину угла OMK. Ответ дайте в градусах.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 62°. Найдите величину угла OMK. Ответ дайте в градусах.
Комментарии: