Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD=10. Докажите, что треугольники CBD и BDA подобны.
ABCD -
трапеция, следовательно, AD||BC.
∠CBD=∠ADB (т.к. это
накрест-лежащие углы для параллельных прямых AD и BC).
Рассмотрим отношения сторон:
BC/BD=5/10=1/2
BD/AD=10/20=1/2
Тогда по
второму признаку подобия треугольников, треугольники CBD и BDA подобны.
Поделитесь решением
Присоединяйтесь к нам...
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник ACP, равен 12 см, тангенс угла ABC равен 2,4. Найдите радиус вписанной окружности треугольника ABC.
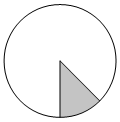Площадь круга равна 88. Найдите площадь сектора этого круга, центральный угол которого равен 45°.
Площадь прямоугольного треугольника равна 50√
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 10. Найдите BC, если AC=16.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 192. Найдите стороны треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: