
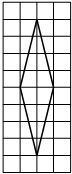
 На клетчатой бумаге с размером клетки 1x1 изображён ромб. Найдите площадь этого ромба.
На клетчатой бумаге с размером клетки 1x1 изображён ромб. Найдите площадь этого ромба.
 Проведем диагонали ромба.
Проведем диагонали ромба.
Диагонали делят ромб на 4 треугольника.
Эти треугольники прямоугольные, так как диагонали пересекаются под прямым углом (по
свойству ромба).
Учитывая второе свойство ромба, получается что у треугольников равны соответственные стороны.
Тогда, эти треугольники равны, по
третьему признаку равенства.
Площадь прямоугольного треугольника:
S=ab/2, где а и b - катеты треугольника.
S=1*4/2=2
Sромб=4S=4*2=8
Ответ: 8
Поделитесь решением
Присоединяйтесь к нам...
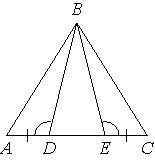 На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
 В треугольнике ABC угол C равен 90°, cosB=5/6, AB=18. Найдите BC.
В треугольнике ABC угол C равен 90°, cosB=5/6, AB=18. Найдите BC.
Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является его медианой.
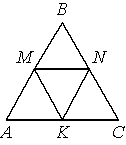 В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равносторонний.
В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равносторонний.
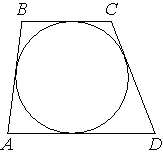 Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=8, CD=12. Найдите AD.
Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=8, CD=12. Найдите AD.
Комментарии: