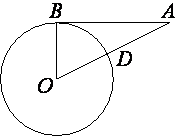
Отрезок AB=32 касается окружности радиуса 24 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
Отрезок AB перпендикулярен OB (по
свойству касательной).
Следовательно, треугольник ABO
прямоугольный.
Тогда можно применить
теорему Пифагора:
AO2=AB2+OB2
AO2=322+242
AO2=1024+576
AO2=1600
AO=40
AO=AD+OD
OD - радиус окружности, следовательно OD=24.
40=AD+24
AD=16
Ответ: 16
Поделитесь решением
Присоединяйтесь к нам...
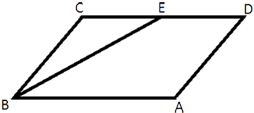Площадь параллелограмма
ABCD равна 30. Точка E – середина стороны CD. Найдите площадь трапеции ABED.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=12, BF=5.
Хорды AC и BD окружности пересекаются в точке P, BP=12, CP=15, DP=25. Найдите AP.
Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите BC, если AB=26.
Сторона ромба равна 36, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: