Хорды AC и BD окружности пересекаются в точке P, BP=12, CP=15, DP=25. Найдите AP.

Другие задачи из этого раздела

Задача №2921C7

Площадь прямоугольного треугольника равна 2450√3/3. Один из острых углов равен 30°. Найдите длину катета, прилежащего к этому углу.

Задача №3B4B4B

В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 136. Найдите стороны треугольника ABC.

Задача №CFAAB6

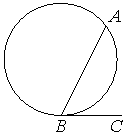На окружности отмечены точки A и B так, что меньшая дуга AB равна 152°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.

Задача №13203A

В трапецию, сумма длин боковых сторон которой равна 24, вписана окружность. Найдите длину средней линии трапеции.

Задача №9A05F7

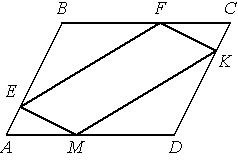В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.