
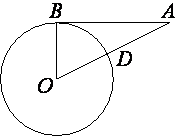
 Отрезок AB=32 касается окружности радиуса 24 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
Отрезок AB=32 касается окружности радиуса 24 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
Отрезок AB перпендикулярен OB (по
свойству касательной).
Следовательно, треугольник ABO
прямоугольный.
Тогда можно применить
теорему Пифагора:
AO2=AB2+OB2
AO2=322+242
AO2=1024+576
AO2=1600
AO=40
AO=AD+OD
OD - радиус окружности, следовательно OD=24.
40=AD+24
AD=16
Ответ: 16
Поделитесь решением
Присоединяйтесь к нам...
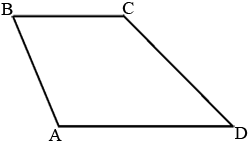 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=32.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=32.
 В треугольнике ABC угол C равен 90°, sinB=4/9, AB=18. Найдите AC.
В треугольнике ABC угол C равен 90°, sinB=4/9, AB=18. Найдите AC.
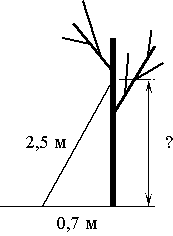 Лестницу длиной 2,5 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 0,7 м?
Лестницу длиной 2,5 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 0,7 м?
 В треугольнике ABC угол C равен 90°, BC=2, sinA=0,2. Найдите AB.
В треугольнике ABC угол C равен 90°, BC=2, sinA=0,2. Найдите AB.
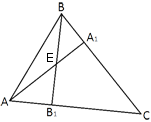 Высоты AA1 и BB1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы AA1B1 и ABB1 равны.
Высоты AA1 и BB1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы AA1B1 и ABB1 равны.
Комментарии: