Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите BC, если AB=26.
BC||AD (по
определению параллелограмма)
∠BAE=∠EAD (т.к. AE -
биссектриса)
∠EAD=∠BEA (т.к. это
накрест-лежащие углы)
Следовательно, ∠BAE=∠BEA
Получается, что треугольник ABE -
равнобедренный (по
свойству), и AB=BE (по
определению равнобедренного треугольника).
Аналогично с треугольником ECD:
∠CED=∠CDE
EC=CD
Так как AB=CD (по
свойству параллелограмма), то получается, что AB=BE=EC=CD=26.
BC=BE+EC=26+26=52.
Ответ: 52
Поделитесь решением
Присоединяйтесь к нам...
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,6 м, если длина его тени равна 8 м, высота фонаря 5 м?
В параллелограмме ABCD точка M — середина стороны AB. Известно, что MC=MD. Докажите, что данный параллелограмм — прямоугольник.
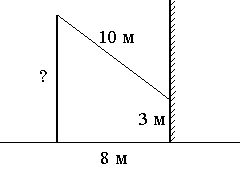От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м.
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=6, AC=10.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: