В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 5:3, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=8.
Рассмотрим треугольник ABF.
По свойству
биссектрисы:
BG/GF=AB/AF=5/3
cosA=AF/AB=3/5 (по
определению косинуса)
Существует тригонометрическая формула:
sin2α+cos2α=1
Тогда:
sin2∠BAF+cos2∠BAF=1
sin2∠BAF+(3/5)2=1
sin2∠BAF=1-9/25
sin2∠BAF=(25-9)/25
sin2∠BAF=16/25
sin∠BAF=4/5
По
теореме синусов:
BC/sin∠BAF=2R
8/(4/5)=8*5/4=10=2R
R=10/2=5
Ответ: 5
Поделитесь решением
Присоединяйтесь к нам...
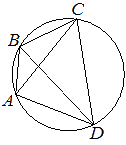Четырёхугольник ABCD вписан в окружность. Угол ABC равен 138°, угол CAD равен 83°. Найдите угол ABD. Ответ дайте в градусах.
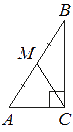В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=60, BC=40. Найдите CM.
Найдите площадь параллелограмма, изображённого на рисунке.
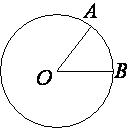На окружности с центром O отмечены точки A и B так, что ∠AOB=40°. Длина меньшей дуги AB равна 50. Найдите длину большей дуги.
Укажите номера верных утверждений.
1) Центры вписанной и описанной окружностей равностороннего треугольника совпадают.
2) Существует квадрат, который не является ромбом.
3) Сумма углов остроугольного треугольника равна 180°.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: