
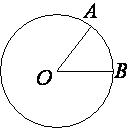
 На окружности с центром O отмечены точки A и B так, что ∠AOB=40°. Длина меньшей дуги AB равна 50. Найдите длину большей дуги.
На окружности с центром O отмечены точки A и B так, что ∠AOB=40°. Длина меньшей дуги AB равна 50. Найдите длину большей дуги.
∠AOB - является
центральным и равен градусной мере дуги, на которую опирается.
Следовательно, градусная мера меньшей дуги AB тоже составляет 40°.
Значит градусная мера большей дуги равна 360°-40°=320°
Пусть х - длина большей дуги, тогда получаем пропорцию:
40° - длина 50
320° - длина х
40/320=50/x
x=320*50/40=8*50=400
Ответ: 400
Поделитесь решением
Присоединяйтесь к нам...
 Радиус окружности, описанной около квадрата, равен 48√2. Найдите радиус окружности, вписанной в этот квадрат.
Радиус окружности, описанной около квадрата, равен 48√2. Найдите радиус окружности, вписанной в этот квадрат.
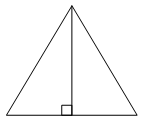 Высота равностороннего треугольника равна 15√
Высота равностороннего треугольника равна 15√
 На отрезке AB выбрана точка C так, что AC=12 и BC=3. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
На отрезке AB выбрана точка C так, что AC=12 и BC=3. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
 В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 9 и 5. Найдите площадь параллелограмма ABCD.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 9 и 5. Найдите площадь параллелограмма ABCD.
 Сторона ромба равна 28, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Сторона ромба равна 28, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Комментарии: