
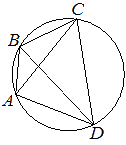 Четырёхугольник ABCD вписан в окружность. Угол ABC равен 138°, угол CAD равен 83°. Найдите угол ABD. Ответ дайте в градусах.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 138°, угол CAD равен 83°. Найдите угол ABD. Ответ дайте в градусах.
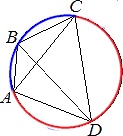 ∠ABC является вписанным углом и опирается на дугу ADC (красная).
∠ABC является вписанным углом и опирается на дугу ADC (красная).
Следовательно, по теореме о вписанном угле, градусная мера дуги ADC равна 138°*2=276°
Тогда градусная мера синей дуги равна 360°-276°=84°
∠ADC тоже является вписанным углом и опирается на дугу ABC (синяя).
Следовательно, по той же теореме о вписанном угле∠ADC=84°/2=42°.
Рассмотрим треугольник ACD.
По теореме о сумме углов треугольника запишем:
180°=∠ADC+∠CAD+∠ACD
180°=42°+83°+∠ACD
180°-42°-83°=∠ACD
∠ACD=55°
 Заметим, что углы ACD и ABD являются вписанными и опираются на одну и ту же дугу.
Заметим, что углы ACD и ABD являются вписанными и опираются на одну и ту же дугу.
Следовательно, эти углы равны, ∠ACD=∠ABD=55°
Ответ: 55
Поделитесь решением
Присоединяйтесь к нам...
 На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=27, MD=18, H — точка пересечения высот треугольника ABC. Найдите AH.
На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=27, MD=18, H — точка пересечения высот треугольника ABC. Найдите AH.
 Один из углов ромба равен 114°. Найдите меньший угол этого ромба. Ответ дайте в градусах.
Один из углов ромба равен 114°. Найдите меньший угол этого ромба. Ответ дайте в градусах.
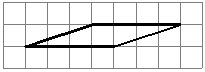 На клетчатой бумаге с размером клетки 1x1 изображён параллелограмм. Найдите его площадь.
На клетчатой бумаге с размером клетки 1x1 изображён параллелограмм. Найдите его площадь.
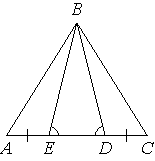 На стороне АС треугольника АВС выбраны точки D и E так, что углы АDB и BEC равны (см. рисунок). Оказалось, что отрезки AЕ и CD тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что углы АDB и BEC равны (см. рисунок). Оказалось, что отрезки AЕ и CD тоже равны. Докажите, что треугольник АВС — равнобедренный.
 Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 16, а площадь равна 32√
Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 16, а площадь равна 32√
Комментарии: