Синус острого угла A треугольника ABC равен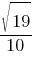 
. Найдите CosA.
Так как нам ничего не известно про треугольник ABC, прямоугольный он или нет и т.д. То остается только воспользоваться основной тригонометрической формулой:
sin2A+cos2A=1
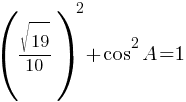
По второму правилу действий со степенями:
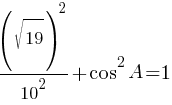
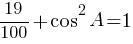
0,19+cos2A=1
cos2A=1-0,19
cos2A=0,81
cosA=√0,81=0,9
Ответ: 0,9
Поделитесь решением
Присоединяйтесь к нам...
Площадь прямоугольного треугольника равна 578√
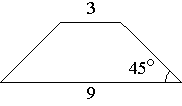В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
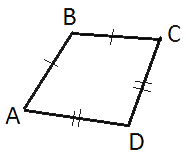В выпуклом четырехугольнике ABCD AB=BC, AD=CD, ∠B=100° , ∠D=104°. Найдите угол A . Ответ дайте в градусах.
Площадь прямоугольного треугольника равна 882√
В трапеции ABCD основания AD и BC равны соответственно 49 и 21, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.
Хочу получать новые решения
Ни какого спама
Автор: Таська
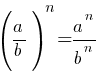
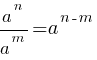
Комментарии: