Сторона квадрата равна 40√2. Найдите радиус окружности, описанной около этого квадрата.
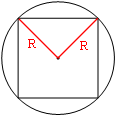Проведем отрезки из центра
квадрата к двум его углам, как на рисунке.
Заметим, что:
1) Эти отрезки и являются радиусами окружности.
2) Получившийся треугольник является
прямоугольным (по свойству квадрата).
Тогда мы можем применить
теорему Пифагора (пусть сторона квадрата - это "а"):
a2=R2+R2
a2=2R2
(40√2)2=2R2
По первому правилу действий со степенями:
402*(√2)2=2R2
402*2=2R2 |:2
402=R2
40=R
Ответ: 40
Поделитесь решением
Присоединяйтесь к нам...
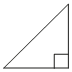В прямоугольном треугольнике один из катетов равен 7, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
Высота BH ромба ABCD делит его сторону AD на отрезки AH=4 и HD=1. Найдите площадь ромба.
Основание AC равнобедренного треугольника ABC равно 18. Окружность радиуса 12 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
Основание AC равнобедренного треугольника ABC равно 8. Окружность радиуса 5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: