Сторона квадрата равна 9√2. Найдите диагональ этого квадрата.
По
первому свойству квадрата, все его углы прямые, следовательно, треугольники, которые образует диагональ, прямоугольные.
Т.е. к этим треугольникам можно применить теорему Пифагора.
По определению квадрата, все его стороны равны, следовательно катеты этих треугольников равны:
d2=(9√2)2+(9√2)2
d2=2(9√2)2
По первому правилу действий со степенями:
d2=2*92(√2)2
d2=2*81*2=324
d=√324=18
Ответ: 18
Поделитесь решением
Присоединяйтесь к нам...
Пол комнаты, имеющей форму прямоугольника со сторонами 7 м и 9 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 20 см. Сколько потребуется таких дощечек?
В окружности с центром в точке О проведены диаметры AD и BC, угол
OAB равен 80°. Найдите величину угла OCD.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 7.
Стороны AC, AB, BC треугольника ABC равны 2√
В прямоугольном треугольнике гипотенуза равна 82, а один из острых углов равен 45°. Найдите площадь треугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
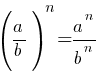
Комментарии: