Радиус окружности, вписанной в прямоугольную трапецию, равен 18. Найдите высоту этой трапеции.
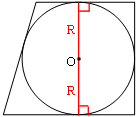Проведем радиусы к точкам касания с основаниями трапеции.
По первому свойству касательной (основания трапеции), она перпендикулярна радиусу.
Так как радиусы одновременно перпендикулярны параллельным основаниям трапеции, то получается, что радиусы представляют из себя единый отрезок или диаметр (это можно доказать если рассмотреть углы при параллельных прямых и секущей. Прямые углы являются односторонними и их сумма равна 180°).
Диаметр и является высотой трапеции:
h=D=2*R=2*18=36
Ответ: 36
Поделитесь решением
Присоединяйтесь к нам...
Пол комнаты, имеющей форму прямоугольника со сторонами 4 м и 10 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 5 см и 20 см. Сколько потребуется таких дощечек?
Радиус окружности, вписанной в трапецию, равен 48. Найдите высоту этой трапеции.
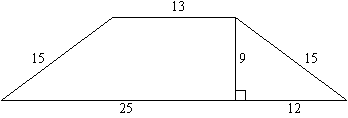Найдите площадь трапеции, изображённой на рисунке.
Какие из данных утверждений верны? Запишите их номера.
1) Любой параллелограмм можно вписать в окружность.
2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.
3) Точка пересечения двух окружностей равноудалена от центров этих окружностей.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 1. Найдите площадь трапеции.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2021-05-28 01:47:57) Марина Степановна Гусаченко: основание прямоугольной трапеции равны 5 и20 см .найти радиус круга вписанного в трапецию