
 Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.
Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.
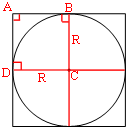 Проведем радиусы окружности к точкам касания со сторонами
квадрата, как показано на рисунке.
Проведем радиусы окружности к точкам касания со сторонами
квадрата, как показано на рисунке.
Обозначим ключевые точки A, B, C и D.
ABCD образует четырехугольник.
В этом четырехугольнике:
∠A=90° (по определению квадрата).
∠B=∠D=90° (по свойству касательной).
Тогда и ∠С=90° (так как сумма углов четырехугольника равна 360°).
Т.е. ABCD - прямоугольник (по
определению).
По свойству прямоугольника:
AB=CD=R
AD=BD=R
Т.е. ABCD - квадрат.
Из рисунка очевидно, что радиус равен половине стороны квадрата:
R=56/2=28
Ответ: 28
Поделитесь решением
Присоединяйтесь к нам...
 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
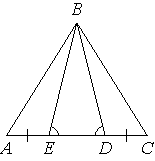 На стороне АС треугольника АВС выбраны точки D и E так, что углы АDB и BEC равны (см. рисунок). Оказалось, что отрезки AЕ и CD тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что углы АDB и BEC равны (см. рисунок). Оказалось, что отрезки AЕ и CD тоже равны. Докажите, что треугольник АВС — равнобедренный.
 Точка О – центр окружности, /BOC=110° (см. рисунок). Найдите величину угла BAC (в градусах).
Точка О – центр окружности, /BOC=110° (см. рисунок). Найдите величину угла BAC (в градусах).
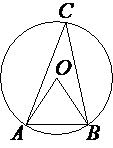 Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 27°.
Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 27°.
 Человек ростом 1,8 м стоит на расстоянии 6 м от столба, на котором висит фонарь на высоте 7,2 м. Найдите длину тени человека в метрах.
Человек ростом 1,8 м стоит на расстоянии 6 м от столба, на котором висит фонарь на высоте 7,2 м. Найдите длину тени человека в метрах.

Комментарии: