
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ736 –Є–Ј 1087 |
–Ъ–∞–Ї–Њ–µ –Є–Ј —Б–ї–µ–і—Г—О—Й–Є—Е —Г—В–≤–µ—А–ґ–і–µ–љ–Є–є –≤–µ—А–љ–Њ?
1) –Т—Б–µ —Г–≥–ї—Л —А–Њ–Љ–±–∞ —А–∞–≤–љ—Л.
2) –Х—Б–ї–Є —Б—В–Њ—А–Њ–љ—Л –Њ–і–љ–Њ–≥–Њ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ —А–∞–≤–љ—Л —Б—В–Њ—А–Њ–љ–∞–Љ –і—А—Г–≥–Њ–≥–Њ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞, —В–Њ —В–∞–Ї–Є–µ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–Є —А–∞–≤–љ—Л.
3) –І–µ—А–µ–Ј –ї—О–±—Г—О —В–Њ—З–Ї—Г, –ї–µ–ґ–∞—Й—Г—О –≤–љ–µ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Љ–Њ–ґ–љ–Њ –њ—А–Њ–≤–µ—Б—В–Є –і–≤–µ –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–µ –Ї —Н—В–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є.
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –Ї–∞–ґ–і–Њ–µ —Г—В–≤–µ—А–ґ–і–µ–љ–Є–µ:
1) "–Т—Б–µ —Г–≥–ї—Л —А–Њ–Љ–±–∞ —А–∞–≤–љ—Л". –†–Њ–Љ–±, —Г –Ї–Њ—В–Њ—А–Њ–≥–Њ –≤—Б–µ —Г–≥–ї—Л —А–∞–≤–љ—Л - —Н—В–Њ —Г–ґ–µ
–Ї–≤–∞–і—А–∞—В. –Э–µ –Ї–∞–ґ–і—Л–є
—А–Њ–Љ–± —П–≤–ї—П–µ—В—Б—П
–Ї–≤–∞–і—А–∞—В–Њ–Љ, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ –і–∞–љ–љ–Њ–µ —Г—В–≤–µ—А–ґ–і–µ–љ–Є–µ –љ–µ–≤–µ—А–љ–Њ.
2) "–Х—Б–ї–Є —Б—В–Њ—А–Њ–љ—Л –Њ–і–љ–Њ–≥–Њ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ —А–∞–≤–љ—Л —Б—В–Њ—А–Њ–љ–∞–Љ –і—А—Г–≥–Њ–≥–Њ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞, —В–Њ —В–∞–Ї–Є–µ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–Є —А–∞–≤–љ—Л" - —Н—В–Њ —Г—В–≤–µ—А–ґ–і–µ–љ–Є–µ –љ–µ–≤–µ—А–љ–Њ. –Ь–Њ–ґ–љ–Њ –њ—А–Є–≤–µ—Б—В–Є –њ—А–Њ—Б—В–Њ–є –њ—А–Є–Љ–µ—А:
–Ї–≤–∞–і—А–∞—В –Є
—А–Њ–Љ–± —Б —А–∞–≤–љ—Л–Љ–Є —Б—В–Њ—А–Њ–љ–∞–Љ–Є - —Б—В–Њ—А–Њ–љ—Л —А–∞–≤–љ—Л, –∞ —З–µ—В—Л—А–µ—Е—Г–≥–Њ–ї—М–љ–Є–Ї–Є –љ–µ —А–∞–≤–љ—Л.
3) "–І–µ—А–µ–Ј –ї—О–±—Г—О —В–Њ—З–Ї—Г, –ї–µ–ґ–∞—Й—Г—О –≤–љ–µ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Љ–Њ–ґ–љ–Њ –њ—А–Њ–≤–µ—Б—В–Є –і–≤–µ –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–µ –Ї —Н—В–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є" - —Н—В–Њ —Г—В–≤–µ—А–ґ–і–µ–љ–Є–µ –≤–µ—А–љ–Њ –њ–Њ
–≤—В–Њ—А–Њ–Љ—Г —Б–≤–Њ–є—Б—В–≤—Г –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є.
–Ю—В–≤–µ—В: 3)
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
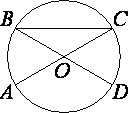 –Т –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ O –Њ—В—А–µ–Ј–Ї–Є AC –Є BD вАФ –і–Є–∞–Љ–µ—В—А—Л. –¶–µ–љ—В—А–∞–ї—М–љ—Л–є —Г–≥–Њ–ї AOD —А–∞–≤–µ–љ 132¬∞. –Э–∞–є–і–Є—В–µ –≤–њ–Є—Б–∞–љ–љ—Л–є —Г–≥–Њ–ї ACB. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Т –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ O –Њ—В—А–µ–Ј–Ї–Є AC –Є BD вАФ –і–Є–∞–Љ–µ—В—А—Л. –¶–µ–љ—В—А–∞–ї—М–љ—Л–є —Г–≥–Њ–ї AOD —А–∞–≤–µ–љ 132¬∞. –Э–∞–є–і–Є—В–µ –≤–њ–Є—Б–∞–љ–љ—Л–є —Г–≥–Њ–ї ACB. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Ь–µ–і–Є–∞–љ–∞ BM —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC —П–≤–ї—П–µ—В—Б—П –і–Є–∞–Љ–µ—В—А–Њ–Љ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –њ–µ—А–µ—Б–µ–Ї–∞—О—Й–µ–є —Б—В–Њ—А–Њ–љ—Г BC –≤ –µ—С —Б–µ—А–µ–і–Є–љ–µ. –Э–∞–є–і–Є—В–µ —Н—В–Њ—В –і–Є–∞–Љ–µ—В—А, –µ—Б–ї–Є –і–Є–∞–Љ–µ—В—А –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC —А–∞–≤–µ–љ 8.
 –І–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї ABCD —Б–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є AB=25 –Є CD=16 –≤–њ–Є—Б–∞–љ –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Ф–Є–∞–≥–Њ–љ–∞–ї–Є AC –Є BD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K, –њ—А–Є—З—С–Љ ∠
AKB=60¬∞. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ —Н—В–Њ–≥–Њ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
–І–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї ABCD —Б–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є AB=25 –Є CD=16 –≤–њ–Є—Б–∞–љ –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Ф–Є–∞–≥–Њ–љ–∞–ї–Є AC –Є BD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K, –њ—А–Є—З—С–Љ ∠
AKB=60¬∞. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ —Н—В–Њ–≥–Њ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
 –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї ABC —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–є —В—А–∞–њ–µ—Ж–Є–Є ABCD, –µ—Б–ї–Є –і–Є–∞–≥–Њ–љ–∞–ї—М AC –Њ–±—А–∞–Ј—Г–µ—В —Б –Њ—Б–љ–Њ–≤–∞–љ–Є–µ–Љ AD –Є –±–Њ–Ї–Њ–≤–Њ–є —Б—В–Њ—А–Њ–љ–Њ–є CD —Г–≥–ї—Л, —А–∞–≤–љ—Л–µ 30¬∞ –Є 80¬∞ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ.
–Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї ABC —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–є —В—А–∞–њ–µ—Ж–Є–Є ABCD, –µ—Б–ї–Є –і–Є–∞–≥–Њ–љ–∞–ї—М AC –Њ–±—А–∞–Ј—Г–µ—В —Б –Њ—Б–љ–Њ–≤–∞–љ–Є–µ–Љ AD –Є –±–Њ–Ї–Њ–≤–Њ–є —Б—В–Њ—А–Њ–љ–Њ–є CD —Г–≥–ї—Л, —А–∞–≤–љ—Л–µ 30¬∞ –Є 80¬∞ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ.
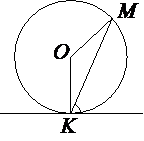 –Я—А—П–Љ–∞—П –Ї–∞—Б–∞–µ—В—Б—П –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –≤ —В–Њ—З–Ї–µ K. –Ґ–Њ—З–Ї–∞ O вАУ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є. –•–Њ—А–і–∞ KM –Њ–±—А–∞–Ј—Г–µ—В —Б –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є —Г–≥–Њ–ї, —А–∞–≤–љ—Л–є 83¬∞. –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ OMK. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Я—А—П–Љ–∞—П –Ї–∞—Б–∞–µ—В—Б—П –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –≤ —В–Њ—З–Ї–µ K. –Ґ–Њ—З–Ї–∞ O вАУ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є. –•–Њ—А–і–∞ KM –Њ–±—А–∞–Ј—Г–µ—В —Б –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є —Г–≥–Њ–ї, —А–∞–≤–љ—Л–є 83¬∞. –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ OMK. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.

–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є: