Найдите площадь квадрата, описанного около окружности радиуса 32.
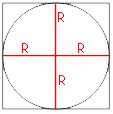Стороны
квадрата являются
касательными к окружности, следовательно, отрезок, проведенный от центра окружности к точке касания будет перпендикулярен стороне
квадрата и равен радиусу окружности (По
свойству касательной).
Получается, что сторона
квадрата равна диаметру окружности, или двум радиусам, т.е. 2*32=64
Площадь
квадрата равна произведению сторон:
S=64*64=4096
Ответ: 4096
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC известно, что AB=8, BC=10, AC=14. Найдите cos∠ABC.
В треугольнике ABC угол C прямой, BC=6, cosB=0,3. Найдите AB.
В треугольнике ABC известно, что ∠BAC=62°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD=25.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=11, CK=20.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: