
 К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=40, AO=85.
К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=40, AO=85.
 Проведем отрезок ОВ.
Проведем отрезок ОВ.
Отрезок OB - это радиус окружности и этот отрезок перпендикулярен AB (по
свойству
касательной).
Следовательно, треугольник AOB -
прямоугольный, тогда, по
теореме Пифагора:
AO2=AB2+OB2
852=402+OB2
7225=1600+OB2
OB2=5625
OB=75=R
Ответ: 75
Поделитесь решением
Присоединяйтесь к нам...
 Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD=10. Докажите, что треугольники CBD и ADB подобны.
Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD=10. Докажите, что треугольники CBD и ADB подобны.
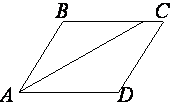 Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 14°. Ответ дайте в градусах.
Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 14°. Ответ дайте в градусах.
 В окружности с центром в точке О проведены диаметры AD и BC, угол
ABO равен 80°. Найдите величину угла ODC.
В окружности с центром в точке О проведены диаметры AD и BC, угол
ABO равен 80°. Найдите величину угла ODC.
Какое из следующих утверждений верно?
1) Один из двух смежных углов острый, а другой тупой.
2) Площадь квадрата равна произведению двух его смежных сторон.
3) Все хорды одной окружности равны между собой.
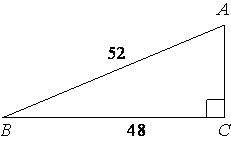 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
Комментарии:
(2019-05-05 11:40:38) Администратор: Коля, Вы имеете ввиду написать само слово \"Дано\"?
(2019-05-05 10:35:58) коля : напишите пожалуста дано спасибо