Найдите площадь квадрата, описанного около окружности радиуса 32.
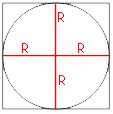Стороны
квадрата являются
касательными к окружности, следовательно, отрезок, проведенный от центра окружности к точке касания будет перпендикулярен стороне
квадрата и равен радиусу окружности (По
свойству касательной).
Получается, что сторона
квадрата равна диаметру окружности, или двум радиусам, т.е. 2*32=64
Площадь
квадрата равна произведению сторон:
S=64*64=4096
Ответ: 4096
Поделитесь решением
Присоединяйтесь к нам...
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=25°. Найдите величину угла BOC. Ответ дайте в градусах.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=8, BF=15.
Из вершины прямого угла C треугольника
ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 8, тангенс угла BAC равен 4/3. Найдите радиус вписанной окружности треугольника ABC.
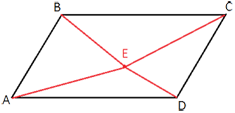Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
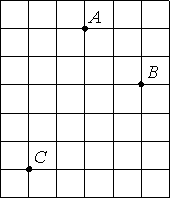На клетчатой бумаге с размером клетки 1см х 1см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: