Постройте график функции y=2x+6|x|-x2 и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
В данной функции присутствуем
модуль, следовательно функцию надо разложить на две подфункции, в зависимости от значения
модуля:
y=2x+6x-x2, при x≥0
y=2x+6(-x)-x2, при x<0
8x-x2, при x≥0
y=-4x-x2, при x<0
Исследуем каждую подфункцию:
1) y=8x-x2
Это квадратичная функция, следовательно график - парабола. Коэффициент а=-1 (т.е. меньше нуля), следовательно ветви параболы направлены вниз. Найдем точки пересечения графика с осью Х, для этого решим уравнение 8x-x2=0
x(8-x)=0
x1=0
x2=8
2) y=-4x-x2
Это квадратичная функция, следовательно график - парабола. Коэффициент а=-1 (т.е. меньше нуля), следовательно ветви параболы направлены вниз. Найдем точки пересечения графика с осью Х, для этого решим уравнение -4x-x2=0
x(-4-x)=0
x1=0
x2=-4
Построим график для каждой подфункции и объединим их.
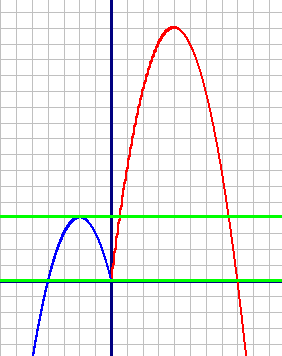1) y1=8x-x2, при x≥0 (красный график)
| X | 0 | 2 | 4 | 6 |
| Y | 0 | 12 | 16 | 12 |
| X | 0 | -1 | -2 | -3 | -4 |
| Y | 0 | 3 | 4 | 3 | 0 |
Поделитесь решением
Присоединяйтесь к нам...
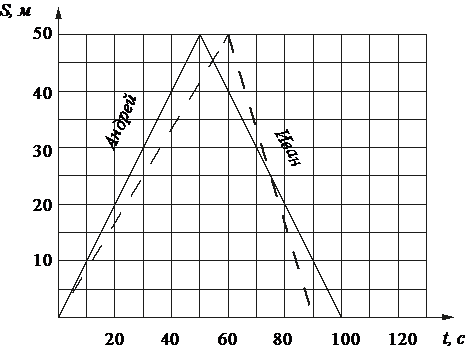Андрей и Иван соревновались в 50-метровом бассейне на дистанции 100 м. Графики их заплывов показаны на рисунке. По горизонтальной оси отложено время, а по вертикальной – расстояние пловца от старта. Кто выиграл соревнование? В ответе запишите, на сколько секунд он обогнал соперника.
Постройте график функции
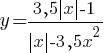
Определите, при каких значениях k прямая y=kx не имеет с графиком общих точек.
Постройте график функции
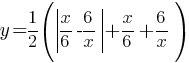
Определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
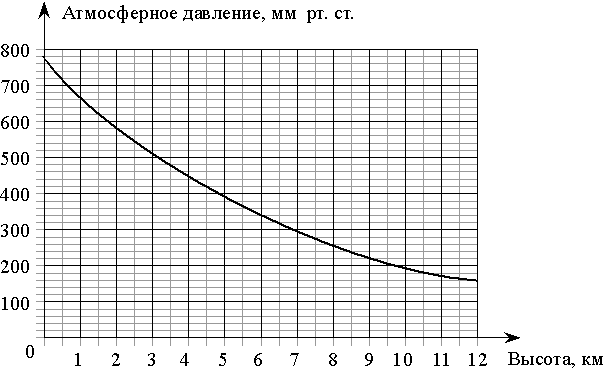На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 220 миллиметров ртутного столба?
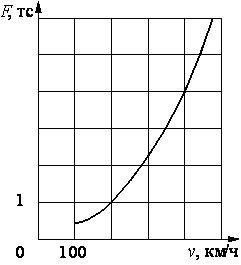Когда самолёт находится в горизонтальном полёте, подъёмная сила, действующая на крылья, зависит только от скорости. На рисунке изображена эта зависимость для некоторого самолёта. На оси абсцисс откладывается скорость (в километрах в час), на оси ординат — сила (в тоннах силы). Определите по рисунку, на сколько увеличится подъёмная сила (в тоннах силы) при увеличении скорости с 200 км/ч до 400 км/ч.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: