
Постройте график функции 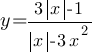 и определите, при каких значениях k прямая y=kx не имеет с графиком ни одной общей точки.
и определите, при каких значениях k прямая y=kx не имеет с графиком ни одной общей точки.
В данной функции присутствуем
модуль, следовательно функцию надо разложить на две подфункции, в зависимости от значения
модуля:
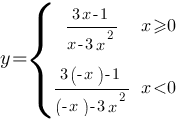
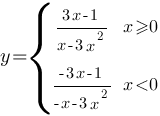
Теперь надо построить график каждой подфункции в его границах и объединить их.
1) 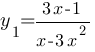 , при х≥0.
, при х≥0.
Напишем Область Допустимых Значений (ОДЗ).
Так как знаменатель не может равняться нулю, то x-3x2≠0 Следовательно:
x(1-3x)≠0
x1≠0
x2≠1/3
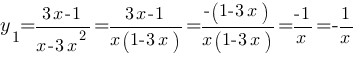
График представляет из себя гиперболу, отметим несколько точек:
| X | 0,5 | 1 | 2 |
| Y | -2 | -1 | -0,5 |
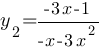 , при х<0.
, при х<0.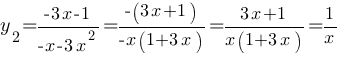
| X | -0,5 | -1 | -2 |
| Y | -2 | -1 | -0,5 |
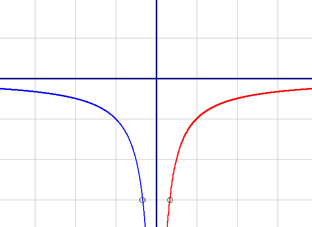 График первой подфункции начерчен красным цветом, второй подфункции - синим.
График первой подфункции начерчен красным цветом, второй подфункции - синим.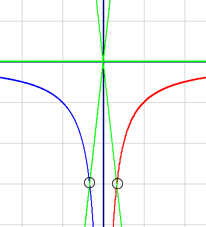
Поделитесь решением
Присоединяйтесь к нам...
Найдите значение выражения (√
Значение какого из данных ниже выражений является иррациональным числом?
1) √18*√8
2) (√22-√7)(√22+√7)
3) 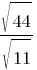
4) √8-4√2
Постройте график функции y=5-(x4-x3)/(x2-x) и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Какое из данных ниже чисел является значением выражения 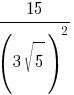
1) 1
2) 1/5
3) 1/3
4) 1/15
В течение августа помидоры подешевели на 40%, а затем в течение сентября подорожали на 70%. Какая цена больше: в начале августа или в конце сентября – и на сколько процентов?
Комментарии: