Постройте график функции y=|x|(x-1)-6x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Данная функция содержит
модуль, следовательно ее нужно разложить на две функции:
x(x-1)-6x, при x≥0
-x(x-1)-6x, при x<0
x2-x-6x, при x≥0
-x2+x-6x, при x<0
x2-7x, при x≥0
-x2-5x, при x<0
Рассмотрим каждую подфункцию:
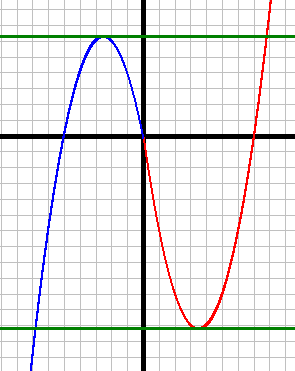1) y=x2-7x, при x≥0 (красный график)
Найдем корни уравнения x2-7x=0, чтобы узнать, в каких точках график пересекает ось х.
x2-7x=0
x(x-7)=0
x1=0
x2=7
| X | 0 | 1 | 2 | 3 |
| Y | 0 | -6 | -10 | -12 |
| X | 0 | -1 | -2 | -3 |
| Y | 0 | 4 | 6 | 6 |
Поделитесь решением
Присоединяйтесь к нам...
Упростите выражение (a-4)2-2a(5a-4) и найдите его значение при a=-1/3. В ответе запишите найденное значение.
Найдите значение выражения (x-5)2-x(10+x) при x=-1/20.
За 5 минут пешеход прошёл a метров. За сколько минут он пройдёт 120 метров, если будет идти с той же скоростью? Запишите соответствующее выражение.
Сколько целых чисел расположено между √13 и √130?
Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние s по формуле s=nl, где n — число шагов, l — длина шага. Какое расстояние прошёл человек, если l=60 см, n=1900? Ответ выразите в километрах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: